Programmes des concours d'admission à l'École normale supérieure Paris-Saclay

Les programmes des concours d'admission en première année et ceux des concours d'admission en deuxième année à l'Ecole normale supérieure de Paris-Saclay sont fixés comme suit :

Titre I. Concours d'admission en première année

Article 1 - Groupes MP (mathématiques, physique) et info-MP (informatique filière MP)

Les programmes des épreuves du concours sont :

a) ceux des classes préparatoires aux grandes écoles 2e année de la filière MP en vigueur l'année du concours ;

b) ceux des classes préparatoires aux grandes écoles 1re année de la filière MPSI en vigueur l'année précédant celle du concours.

Les candidats doivent connaître les notions du programme du baccalauréat général nécessaires à la compréhension des programmes définis ci-dessus.

 

Article 2 - Groupe info-MPI (informatique filière MPI)

Les programmes des épreuves du concours info-MPI sont :

a) ceux des classes préparatoires aux grandes écoles 2e année de la filière MPI en vigueur l'année du concours ;

b) ceux des classes préparatoires aux grandes écoles 1re année de la filière MP2I en vigueur l'année précédant celle du concours.

Les candidats doivent connaître les notions du programme du baccalauréat général nécessaires à la compréhension des programmes définis ci-dessus.

 

Article 3 - Groupe PC (physique, chimie)

Les programmes des épreuves du concours sont :

a) ceux des classes préparatoires aux grandes écoles 2e année de la filière PC en vigueur l'année du concours ;

b) ceux des classes préparatoires aux grandes écoles 1re année de la filière PCSI en vigueur l'année précédant celle du concours.

Les candidats doivent connaître les notions du programme du baccalauréat de l'enseignement secondaire nécessaires à la compréhension des programmes définis ci-dessus.

 

Article 4 - Groupe BCPST (biologie, chimie, physique, sciences de la Terre)

Les programmes des épreuves du concours sont :

a) ceux des classes préparatoires aux grandes écoles 2e année de la filière BCPST en vigueur l'année du concours ;

b) ceux des classes préparatoires aux grandes écoles 1re année de la filière BCPST en vigueur l'année précédant celle du concours.

Les candidats doivent connaître les notions du programme du baccalauréat général nécessaires à la compréhension des programmes définis ci-dessus.

 

Article 5 - Groupe PSI (physique, sciences de l'ingénieur)

Les programmes des épreuves du concours sont :

a) ceux des classes préparatoires aux grandes écoles 2e année de la filière PSI en vigueur l'année du concours ;

b) ceux des classes préparatoires aux grandes écoles 1re année de la filière PCSI en vigueur l'année précédant celle du concours.

Les candidats doivent connaître les notions du programme du baccalauréat général nécessaires à la compréhension des programmes définis ci-dessus.

 

Article 6 - Groupe PT (physique, technologie)

Les programmes des épreuves du concours sont :

a) ceux des classes préparatoires aux grandes écoles 2e année de la filière PT en vigueur l'année du concours ;

b) ceux des classes préparatoires aux grandes écoles 1re année de la filière PTSI en vigueur l'année précédant celle du concours.

Les candidats doivent connaître les notions du programme du baccalauréat général nécessaires à la compréhension des programmes définis ci-dessus.

Le concours de l'ENS Paris-Saclay respecte toutes les consignes réglementaires de la banque nationale d'épreuves PT.

 

Article 7 - Groupe TSI (technologie et sciences industrielles)

Les programmes des épreuves du concours sont :

a) ceux des classes préparatoires aux grandes écoles 2e année de la filière TSI en vigueur l'année du concours ;

b) ceux des classes préparatoires aux grandes écoles 1re année de la filière TSI en vigueur l'année précédant celle du concours.

Les candidats doivent connaître les notions du programme du baccalauréat général nécessaires à la compréhension des programmes définis ci-dessus.

Le concours de l'ENS Paris-Saclay respecte toutes les consignes réglementaires de la banque TSI gérée par les concours communs polytechniques.

 

Article 8 - Groupe post-DUT-BTS (options GC-GE-GM)

Le programme de l'épreuve de mathématiques a pour objectif d'évaluer les connaissances des candidats et de vérifier la maîtrise des outils mathématiques nécessaires à l'intégration en première année d'un département des sciences pour l'ingénieur de l'ENS Paris-Saclay sur les items suivants :

• algèbre linéaire ;
• calcul différentiel, équations différentielles, primitives et calcul intégral ;
• trigonométrie et nombres complexes (pour les filières où ils sont au programme) ;
• suites et séries (pour les filières où elles sont au programme) ;
• transformée de Fourier (pour les filières où elle est au programme).

Le programme de l'épreuve pratique d'admission est propre à l'option choisie lors de l'inscription

Pour la filière génie civil (GC), le candidat sera confronté à un système réel dont il devra vérifier des caractéristiques et des performances, par exemple (liste non exhaustive) :

• étude de la résistance au cisaillement des sols ;
• validation des performances d'un système triangulé ;
• étude des caractéristiques mécaniques d'un béton durci ;
• étude du rayonnement dans le visible ;
• étude des pertes de charge d'un réseau hydraulique.

Pour la filière génie électrique (GE), afin de tenir compte des programmes des différents cursus suivis par les candidats, le sujet de l'épreuve portera principalement sur deux (seulement) des 3 grands thèmes suivants :

• électronique ;
• conversion d'énergie ;
• informatique industrielle.

Pour la filière génie mécanique (GM), le candidat sera confronté à un système mécanique sur lequel il pourra :

• expliquer le fonctionnement d'un système de transformation de mouvement ou de réduction à partir d'un schéma cinématique ;
• valider le cas échéant des rapports de réduction de trains simples ou épicycloïdaux ;
• réaliser une étude statique et/ou cinématique par une méthode analytique ou graphique ;
• valider le dimensionnement de composants par des calculs de RdM ;
• justifier des choix de matériaux et de solutions constructives pour le guidage en rotation.

 

Article 9 - Design

ÉPREUVES ÉCRITES D'ADMISSIBILITÉ

Épreuve de dissertation de philosophie générale de l'art

Sans programme limitatif.

Il ne s'agit pas ici de témoigner d'une connaissance érudite de l'histoire de la philosophie mais de faire preuve d'une culture philosophique fondamentale et des capacités méthodologiques indispensables : savoir organiser une pensée, savoir rédiger, savoir questionner. Une liste de notions ne saurait être donnée pour programme. Les notions esthétiques fondamentales doivent être connues (le beau, le sublime, l'art, la forme) et les questions telles que celles de la perception, de la tradition, de l'histoire, de la culture, de la cité notamment doivent pouvoir être interrogées.

Épreuve de dissertation d'histoire de l'art

Sur un programme spécifique faisant l'objet d'un arrêté au BOESR renouvelé tous les deux ans, qui tente de lier l'histoire de l'art générale à l'histoire spécifique des arts appliqués et qui peut jouer d'amplitudes temporelles variables, le candidat doit témoigner d'une connaissance de la question et d'une culture visuelle ou technique. Il doit organiser ses acquis autour d'une problématisation correctement rédigée et faire alternativement jouer ses capacités analytiques et ses qualités de synthèse.

Épreuve de techno-design

Cette épreuve à dominante expression graphique vise à identifier la capacité du candidat à observer un procédé ou un système de mise en œuvre de façon critique et créative.

L'usage du dessin est attendu d'une part pour ses qualités documentaires, techniques, descriptives et d'autre part pour soutenir une écriture, éventuellement multiple, qu'impose l'exposé de procédés et de matériaux à travers leurs interactions.

L'épreuve consiste d'abord en une analyse de documents technologiques (comprenant notamment des procédés de production ou des structures de construction), historiques, scientifiques et issus du champ des arts et des arts appliqués. Elle repose sur la mise en forme de quelques hypothèses quant au possible réinvestissement des données de l'analyse en situation de projet.

Cette exploitation créative, issue d'un regard critique sur une série de documents est l'objectif essentiel de l'exercice. Il s'agit d'apprécier la mobilité intellectuelle du candidat dans un champ de contraintes finement observées, contextualisées et organisées pour initier des potentialités variées et avancées.

ÉPREUVES D'ADMISSION

Épreuve pratique de design

Épreuve pratique de design, option design espace puis soutenance

Épreuve pratique :

L'épreuve consiste en un avant-projet portant sur la conception d'un dispositif spatial destiné à être intégré dans un environnement déterminé (espace naturel ou urbain, privé ou public, espace de communication à caractère culturel, commercial ou institutionnel). L'étude demandée indique le contexte dans lequel la demande s'exerce, la nature de ce dispositif, sa fonction, sa destination, l'environnement dans lequel il doit s'intégrer, les techniques et matériaux (soit imposés, soit laissés au choix du candidat) avec lesquels il peut être réalisé.

Elle comporte :

• la recherche de l'élément demandé ;
• sa mise en situation dans son environnement (physique, de communication, etc.).

Il est demandé au candidat d'établir les documents nécessaires à la compréhension de l'avant-projet, tels que : schémas et croquis, esquisses graphiques et colorées, plans géométraux et coupes, vues de détail, vues perspectives d'ambiance en noir ou en couleur, bref énoncé des motivations et de la justification des choix.

Épreuve orale :

À l'aide de ses épreuves et répondant aux questions des membres du jury, le candidat défend la conception qu'il propose.

Épreuve pratique de design, option design produit puis soutenance

Épreuve pratique :

L'épreuve consiste en un avant-projet portant sur :

• la conception d'un objet destiné à être produit industriellement ;
• l'identification et/ou la promotion de ce produit.

L'étude demandée se fait à partir d'un cahier des charges restreint comprenant :

• la description du produit à concevoir (fonctions à assurer, qualités et performances visées) ;
• sa destination ;
• les attentes de l'utilisateur.

Elle comportera la recherche du produit, prenant en compte des impératifs tenant à sa fonction, à son usage et à son image. Selon la logique des sujets, il peut être demandé en complément la recherche d'un élément de communication visuelle se rapportant au produit conçu. Il est demandé au candidat d'établir, sous forme d'un dossier d'étude, les documents nécessaires à la compréhension de l'avant-projet, tels que schémas et croquis, esquisses graphiques et colorées, vues cotées de l'objet, plans et vues significatives, vues perspectives, bref énoncé des motivations et de la justification des choix.

L'épreuve peut donner lieu à une vérification de notions élémentaires en ergonomie (rapports dynamiques du corps avec le produit) fondée sur les connaissances nécessaires en anatomie et anthropométrie.

Épreuve orale :

À l'aide de ses épreuves et répondant aux questions des membres du jury, le candidat défend la conception qu'il propose.

Épreuve pratique de design, option design graphique puis soutenance

Épreuve pratique :

L'épreuve consiste en l'analyse d'une commande dans le champ de la communication visuelle (édition ou multimédia) et le développement d'un avant-projet graphique. À partir d'un cahier des charges précisant le contenu du projet, ses fonctions, son contexte ainsi que les conditions de sa diffusion, le candidat doit concevoir un dispositif graphique dans sa globalité (identité visuelle, campagne de communication, site internet, édition, etc.). Le projet doit prendre en compte les contraintes techniques et technologiques de production (soit imposées, soit laissées au choix du candidat).

Elle comporte :

• l'analyse de la commande ;
• les recherches de propositions ;
• la conception d'un projet de communication visuelle et sa mise en situation ;
• l'ensemble des choix et des hypothèses devra être justifié ;
• le candidat doit mobiliser tous les modes de communication graphique pour rendre compte du fonctionnement technique et conceptuel du projet (schémas et croquis, esquisses graphiques et colorées, etc.).

Épreuve orale :

À l'aide de ses épreuves et répondant aux questions des membres du jury, le candidat défend la conception qu'il propose.

Portfolio personnel : documenter, peindre et dessiner puis soutenance

Il est demandé au candidat d'éditer son travail afin de donner une idée de son profil créatif au moyen d'un objet éditorial, photocopié, imprimé ou digital.

Le dossier comprend obligatoirement une note dactylographiée, articulée au contenu et spécifiquement pensée comme une analyse de son choix des médiums pratiqués, de leurs puissances propres, de leur histoire et de leur impact contemporain.

Soutenance :

Le candidat expose une sélection courte et représentative de son travail, de son écriture et de ses démarches.

 

Article 10 - Économie et gestion

Option I : option économique et de gestion.

Option II : option économique et commerciale générale.

ÉPREUVES ÉCRITES D'ADMISSIBILITÉ, OPTION I

Composition de mathématiques et statistiques

A. Éléments de logique

La logique nécessaire pour l'argumentation et la démonstration mathématique est travaillée transversalement sans que sa maîtrise soit un attendu de la formation, dans la continuité des intentions du programme de mathématiques complémentaires. Cela ne doit pas faire l'objet d'un exposé théorique. Les étudiants apprennent ou perfectionnent la pratique en situation de :

• l'utilisation des connecteurs logiques « et », « ou » ;
• l'utilisation du quantificateur universel ;
• l'identification dans le cas d'une proposition conditionnelle de la proposition directe, sa réciproque, et sa négation ;
• l'utilisation des expressions « condition nécessaire », « condition suffisante » ;
• la formulation de la négation d'une proposition ;
• l'utilisation d'un contre-exemple pour infirmer une proposition universelle ;
• l'utilisation explicite des types de raisonnement spécifiques : raisonnement par disjonction des cas, recours à la contraposée, raisonnement par l'absurde, raisonnement par récurrence.

On introduit les symboles de somme Σ et le produit Π dans le cas fini.

B. Ensemble et combinatoire

B. 1. Ensemble

• opérations élémentaires sur les parties d'un ensemble : intersection, réunion,  complémentation ;
• ensemble des parties d'un ensemble, inclusion, partition ;
• produit cartésien d'un nombre fini d'ensembles.

B. 2. Relations binaires

• définition, propriétés : réflexibilité, symétrie, antisymétrie, transitivité ;
• graphe d'une relation ;
• ordre, relation d'équivalence, classes d'équivalence. Application à la relation de préférence et aux classes d'indifférence ;
• notions de majorant, de minorant, de plus grand élément, de plus petit élément.

B. 3. Applications

• injection, surjection, bijection.

B. 4. Combinatoire

L'objectif est de fournir aux étudiants les outils de combinatoire nécessaires pour les calculs probabilistes.

• nombre d'applications d'un ensemble fini dans un autre ;

• permutation, arrangement, combinaison ;

• coefficient binomial, factorielle ; 

•

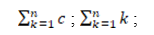
• formule du binôme.

C. Algèbre linéaire

C. 1. Espace vectoriel Rⁿ  

• famille de vecteurs : combinaison linéaire, sous-espace vectoriel ;

• indépendance linéaire, base, dimension ;

• application linéaire, noyau et image d'une application linéaire. Matrice d'une application linéaire ;

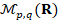• , opérations sur les matrices. Transposition d'une matrice. Matrices inversibles. Matrices symétriques.

C. 2. Systèmes d'équations linéaires

• écriture matricielle, système de Cramer, résolution par la méthode du pivot de Gauss ;
• rang d'une matrice.

C. 3. Réduction

• valeur propre d'une matrice, vecteur propre, sous-espace propre associé ;
• matrices diagonales, matrices diagonalisables, exemples de diagonalisation ;
• une matrice de taille n ayant n valeurs propres distinctes est diagonalisable (théorème admis) ;
• une matrice symétrique est diagonalisable (théorème admis).

D. Analyse mathématique

D. 1. Suites

• intervalle ouvert, intervalle fermé. Exemples d'ensembles ouverts, ensembles fermés définis par des systèmes d'inéquations ;
• suites de nombres réels. Suites croissantes, suites décroissantes ;
• suites usuelles : suites arithmétiques et géométriques. L'étude d'une suite arithmético-géométrique doit être guidée vers l'étude d'une suite géométrique ;
• limite d'une suite. Théorème d'encadrement par des suites convergentes de même limite (théorème des gendarmes), théorème de la limite monotone (théorèmes admis).

D. 2. Fonctions de R dans R

• limite d'une fonction en un point. Continuité (tout exposé théorique sur ce sujet est à exclure) ;
• étude des fonctions numériques : dérivée, tableau de variation, représentation graphique. Recherche d'extrema locaux et globaux. Exemples d'études d'asymptotes ;
• fonctions usuelles : linéaire, polynômes, logarithmique, exponentielle, puissance, valeur absolue ;
• théorème de Rolle (sans démonstration), formule de Taylor, développements limités d'ordre 1 ou 2, allure locale du graphe d'une fonction en un point ;
• croissances comparées ;
• fonctions convexes deux fois continûment dérivables.

D. 3. Fonctions de Rⁿ dans R

• dérivées partielles, points critiques ;
• matrice hessienne, formule de Taylor d'ordre 2 (sans démonstration) ;
• fonctions concaves, convexes ;
• recherche d'extrema locaux : conditions nécessaires, conditions suffisantes ;
• recherche d'extrema locaux sous contrainte homogène. Méthode des multiplicateurs de Lagrange.

D. 4. Intégration dans R

• intégrale d'une fonction positive sur un segment, généralisation à une fonction de signe quelconque ;
• utilisation des fonctions primitives pour le calcul des intégrales ;
• intégrale généralisée (définition et exemples) ;
• intégration par parties.

E. Statistique descriptive

Ces notions gagnent à être illustrées par des exemples tirées d'autres disciplines.

E. 1. Analyse statistique d'une variable

• définition d'une variable statistique : population, caractères, modalités ;
• effectifs, fréquence, fréquences cumulées ;
• représentations graphiques ;
• caractéristiques de position : mode, médiane, quantile, moyenne ;
• caractéristiques de dispersion dans le cas où l'ensemble des modalités est R : étendue ; intervalles  interquartiles ; variance, écart-type, coefficient de variation.

E. 2. Analyse statistique de deux variables ; tri croisé :

• tableau d'effectifs, fréquences marginale et conditionnelle ;
• covariance, coefficient de corrélation linéaire, ajustement linéaire par la méthode des moindres carrés.

F. Éléments de théorie de probabilités

F. 1. Généralités

• expérience aléatoire, événements, système complet d'événements ;

• définition mathématique de la probabilité ;

• probabilités conditionnelles. Notation 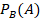, formule des probabilités totales, formule de Bayes ;

• indépendance en probabilité d'événements.

F. 2. Variables aléatoires

• définition d'une variable aléatoire à valeurs réelles ou plus généralement à valeurs dans  Rⁿ ;
• variables aléatoires réelles discrètes :
  • loi de probabilité. Fonction de répartition Fₓ (x) = P (X ≥ x). Espérance ou moyenne. Variable centrées,
  • variable aléatoire Y=g(X) fonction d'une variable aléatoire discrète, où g est définie sur l'ensemble des valeurs prises par X,
  • variance, écart-type, moment d'ordre 2, variables réduites ;
• vecteurs aléatoires discrets (à valeurs dans  Rⁿ) :
  • loi de probabilité d'un vecteur à valeur dans Rⁿ,
  • lois marginales, lois conditionnelles,
  • indépendance de deux variables aléatoires réelles ;
• indépendance de n variables aléatoires réelles :
  • espérance mathématique du produit de deux variables aléatoires indépendantes,
  • variance d'une somme de variables aléatoires indépendantes,
  • covariance, coefficient de corrélation linéaire, variance d'une somme de deux variables aléatoires ;
• lois discrètes usuelles : loi certaine, loi de Bernoulli, binomiale, hypergéométrique, géométrique, de Poisson (propriétés admises) ;
• variables aléatoires à densité :
  • définition d'une densité de variable aléatoire. Exemples simples de fonctions d'une variable aléatoire, tels que aX + b, X2, exp X,
  • espérance ou moyenne. Variables centrées,
  • variance, écart-type. Moment d'ordre 2. Variables centrées réduites ;
  • lois définies par une densité usuelle : loi uniforme, exponentielle, normale (ou de Laplace-Gauss).

F. 3. Estimation

• échantillonnage ;
• risque quadratique ;
• estimateur, biais d'un estimateur ;
• estimation ponctuelle d'une proportion. Loi faible des grands nombres (sans démonstration).

Composition d'analyse microéconomique

Théorie du consommateur

• modélisation du comportement de consommation : relation de préférence et fonction d'utilité ;
• équilibre du consommateur : maximisation de l'utilité, minimisation de la dépense, dualité ;
• statique comparative (équation de Slutsky) ;
• applications : choix intertemporel ; arbitrage travail-loisir.

Théorie du producteur

• description de la technologie, fonction de production ;
• équilibre du producteur en concurrence pure et parfaite : maximisation du profit et minimisation du coût.

Équilibre concurrentiel

• équilibre partiel en concurrence pure et parfaite ;
• notion de surplus économique, de variation de surplus : réglementation, taxation ;
• équilibre général de concurrence : économie d'échange pur, économie de production ;
• optimum de Pareto et théorèmes de l'économie du bien-être.

Concurrence imparfaite

• notions élémentaires de théorie des jeux : stratégie dominante, équilibre de Nash, dilemme du prisonnier. Les candidats devront être capables de raisonner en utilisant ces outils fondamentaux dans un cadre impliquant 2 joueurs et 2 stratégies pour chaque joueur ;
• monopole (simple, naturel, discriminant) ;
• oligopoles (Cournot, Bertrand, Stackelberg, cartel) ;
• concurrence monopolistique.

Défaillances de marché

• biens collectifs : équilibre de souscription volontaire, condition de Bowen-Lindahl-Samuelson, équilibre de Lindahl ;
• externalités, incitations à la Pigou, création de droits de propriété ;
• notions élémentaires sur l'asymétrie d'information : aléa moral, antisélection. Il s'agira, pour les candidats, de bien comprendre les logiques économiques sous-jacentes à ces deux concepts et d'être capables d'identifier les situations économiques correspondantes.

Composition d'analyse macroéconomique

Les grandes fonctions de la macroéconomie

• répartition du revenu : consommation et épargne ;
• production, capital et investissement ;
• travail, emploi et chômage.

L'analyse monétaire et financière

• monnaie, prix et inflation ;
• financement de l'économie ;
• marchés financiers.

L'équilibre macroéconomique et l'analyse des politiques économiques

• justifications et limites de l'intervention de l'État dans l'économie ;
• politiques économiques : nature, objectifs et instruments ;
• modèles d'équilibre macroéconomique de court-terme : IS/LM, IS/LM/BP, AS/AD.

L'économie internationale

• principales théories du commerce international ;
• régimes de change et déterminants des taux de change ;
• système monétaire et financier international ;
• union monétaire et zone monétaire optimale.

Épreuve à option à dominante gestion

Étude de cas portant sur l'option à dominante gestion.

Notions fondamentales.

Les principes comptables.

Méthodologie comptable : la comptabilité en partie double ; le jeu des comptes ; le bilan ; les charges et les produits ; le résultat comptable.

Cadre conceptuel et normalisation.

Les opérations de fin d'exercice : inventaire, bilan, compte de résultat.

Documents d'analyse des résultats et des flux.

Notions sur le calcul des coûts.

L'analyse des charges d'exploitation : charges directes et indirectes ; charges d'activité et charges de structure.

Les méthodes de calcul des coûts : coûts complets (méthode des centres d'analyse et des coûts à base d'activité).

Éléments d'optimisation pour la gestion d'entreprise.

Gestion financière.

Analyse de la rentabilité et de la structure financière.

Notion d'actualisation et critères de choix des investissements.

Notions de valeur de l'entreprise.

Théorie des organisations économiques.

La nature des organisations économiques : institutions, coûts de transaction, droits de propriété, relation d'agence.

Choix stratégiques et éléments d'économie industrielle.

Notions élémentaires sur les systèmes d'information.

Incitations, motivations, culture d'entreprise.

Notions d'efficience interne de l'entreprise.

Épreuve à option à dominante économique

Histoire économique et sociale des principaux pays industrialisés au XXe siècle

• histoire économique des nations européennes et des États-Unis d'Amérique de la Première à la Seconde Guerre mondiale ;
• développement économique, démographie, inégalités et chômage, en Allemagne, aux États-Unis, en France, au Royaume-Uni, au Japon et en Chine de la Seconde Guerre mondiale au tournant du XXIe ;
• les politiques sociales, l'État Providence : développement et limites.

Histoire économique de l'ex-bloc soviétique et des pays émergents

Les anciens États à économie planifiée

• l'épuisement du modèle de développement des systèmes économiques centralisés : Union Soviétique et Chine.

Les pays émergents

• bilan économique de la colonisation et de la décolonisation ;
• la différenciation du développement et l'éclatement de la notion de tiers monde : émergence des nouveaux pays industrialisés et de la Chine ;
• le modèle de développement économique de l'Asie orientale et du Sud-Est ;
• la persistance de la sous-industrialisation et de la pauvreté dans les pays les plus pauvres ;
• indicateurs de croissance, développement et d'insertion dans le commerce international.

Évolution de l'économie internationale : mondialisation et régionalisation

L'Union européenne

• histoire des communautés européennes de 1950 à la crise de 2008 : politique tarifaire, politique énergétique, politique technologique, politique de la concurrence, politique agricole commune, politique monétaire européennes ;
• l'élargissement de l'UE et les enjeux liés à l'intégration européenne dans la première décennie du 21e siècle

L'OMC et les échanges internationaux

• la recherche d'un nouvel ordre économique international. Les zones économiques régionales et l'évolution de l'économie internationale. La mise en place et le fonctionnement de l'OMC ;
• l'évolution du partage international du travail, délocalisations, éclatement des systèmes productifs, enjeux de souveraineté et maîtrise des technologies clés ;
• débats sur la désindustrialisation des pays européens et de l'Amérique du Nord ;
• le développement des transports et des systèmes d'information, effet sur la structure des entreprises et la décomposition des processus productifs ;
• les marchés internationaux de produits agricoles et des matières premières.

Financiarisation des économies jusqu'à la crise de 2008

• les dynamiques non linéaires de financiarisation des économies et leurs conséquences ;
• évolution des systèmes monétaires et financiers au XXe siècle ;
• les enseignements des crises monétaires et financières au XXe siècle.

Enjeux environnementaux au XXe siècle

• impact du développement économique sur l'environnement : de la prise de conscience aux prémices de l'action.

ÉPREUVES ORALES D'ADMISSION

OPTION I : option économique et de gestion

Langue vivante étrangère 

L'épreuve de langue vivante étrangère porte au choix du candidat sur l'une des langues vivantes suivantes : allemand, anglais, espagnol, italien, russe.

L'épreuve orale comporte le compte rendu organisé et le commentaire d'un document radiophonique authentique d'une durée comprise entre 3 minutes 30 et 4 minutes.

Les documents abordent des sujets contemporains et portent sur les problématiques politiques, économiques, culturelles et sociales spécifiques aux domaines linguistiques concernés.

L'usage d'un dictionnaire est interdit.

Interrogation d'analyse économique

L'interrogation porte sur l'intégralité du programme des épreuves écrites d'analyse microéconomique et d'analyse macroéconomique. Les candidats devront, en outre, être capables de replacer les principales théories dans le cadre général de l'histoire de la pensée économique et d'illustrer ces théories par des exemples puisés dans les faits économiques contemporains.

OPTION II : option économique et commerciale générale (ECG)

Interrogation de mathématiques

Le programme de l'épreuve correspond au programme proposé en classe préparatoire ECG.

Interrogation de spécialité

Le programme de l'épreuve correspond au programme proposé en classe préparatoire ECG.

ÉPREUVE COMMUNE AUX OPTIONS I ET II

Épreuve d'entretien

L'épreuve d'entretien prend la forme d'un exposé du candidat à partir d'un texte à caractère général suivi de questions permettant d'apprécier :

• l'aptitude du candidat à s'exprimer correctement et à communiquer ;
• l'aptitude du candidat à dégager pour l'essentiel le sens et l'intérêt des documents à l'étude et à manifester une réaction personnelle.

 

Article 11 - Sciences sociales

Le programme est celui des classes préparatoires de lettres et sciences sociales première et seconde année.

Le programme de l'épreuve écrite de mathématiques est le programme de mathématiques des classes préparatoires aux grandes écoles, filière littéraire, voie B/L, défini par l'arrêté du 25 novembre 2016 modifiant l'arrêté du 25 mars 2013 relatif aux objectifs de formation des classes préparatoires littéraires aux grandes écoles lettres et sciences sociales, paru au BOESR n° 1 du 5 janvier 2017.

Le programme de l'épreuve écrite de sciences sociales est le programme de sciences sociales des classes préparatoires aux grandes écoles, filière littéraire, voie B/L, défini par l'arrêté du 16 mars 2017 modifiant l'arrêté du 25 mars 2013 relatif aux objectifs de formation des classes préparatoires littéraires aux grandes écoles lettres et sciences sociales, paru au JORF n° 0077 du 31 mars 2017.

 

Article 12 - Langue étrangère : anglais

Le programme des épreuves écrites est le même que celui des classes préparatoires de lettres première et seconde année de l'École normale supérieure de Lyon.

L'épreuve orale d'admission « épreuve de civilisation portant sur un document de langue anglaise, suivie d'un entretien » porte sur un programme limitatif de culture générale moderne renouvelé tous les deux ans. Ce programme spécifique fait l'objet d'un arrêté au BOESR.

 

Article 13 - TB (technologie et biologie)

Les programmes des épreuves du concours sont :

a) ceux des classes préparatoires aux grandes écoles 2e année de la filière TB en vigueur l'année du concours ainsi que le programme de SVT de 2e année de la filière BCPST ;

b) ceux des classes préparatoires aux grandes écoles 1re année de la filière TB en vigueur l'année précédant celle du concours ainsi que le programme de SVT de 1re année de la filière BCPST.

Les candidats devront connaître les notions du programme du baccalauréat de l'enseignement secondaire nécessaires à la compréhension des programmes définis ci-dessus.

Titre II. Programme des concours d'admission en deuxième année

Article 14 - Épreuve écrite de français et de culture générale

L'épreuve de français et de culture générale, épreuve écrite d'admission du concours mathématiques consiste en un résumé d'un texte de culture générale. À partir d'une question se rattachant au texte, le candidat doit construire une réponse argumentée et personnelle permettant d'apprécier son aptitude à dégager le sens et l'intérêt d'un texte.

Une grande importance est accordée aux qualités de forme : logique de la composition, correction et précision du style.

 

Article 15 - Épreuve orale d'entretien

L'épreuve d'entretien prend la forme d'un exposé du candidat à partir d'un texte d'intérêt général ou scientifique suivi de questions permettant d'apprécier son aptitude à s'exprimer clairement, à dégager le sens et l'intérêt du texte, à manifester une réaction personnelle. L'échange doit aussi permettre au candidat de préciser ses motivations et son projet de formation par référence au dossier d'études supérieures adressé pour la phase de sélection.

 

Article 16 - Mathématiques

Programme de l'épreuve de mathématiques générales et de l'épreuve orale de mathématiques

I. Topologie

1. Espaces topologiques, espaces séparés, espaces compacts, espaces localement compacts. Espaces connexes. Composantes connexes. Topologie de R. Limites. Applications continues, homéomorphismes. Applications continues définies sur un espace compact. Produits d'espaces topologiques en nombre fini. Espaces métriques, suites. Applications uniformément continues. Suites de Cauchy, espaces complets, complétés d'un espace métrique. Théorème du point fixe contractant. Norme de la convergence uniforme ;

2. Espace vectoriel normé, espace de Banach, espace dual. Norme d'une application linéaire continue. Espace de Hilbert. Projection sur un convexe fermé. Projection orthogonale sur un sous-espace vectoriel fermé. Dual d'un Hilbert. Théorème de représentation de Riesz. Familles orthonormées. Bases Hilbertiennes (cas séparable). Égalité de Bessel-Parseval ;

3. Continuité des fonctions d'une ou plusieurs variables à valeurs dans Rn. Propriétés des fonctions continues sur un compact, sur un connexe. Homéomorphismes d'un intervalle de R. Fonctions réciproques. Fonctions monotones ;

4. Fonctions convexes d'une variable, inégalités de convexité.

II. Calcul différentiel

1. Fonctions réelles d'une variable réelle, dérivée en un point, dérivée à gauche, à droite. Dérivées d'ordre supérieur, dérivée n-ième du produit de deux fonctions. Théorème de Rolle, théorème des accroissements finis. Formules de Taylor : différentes formes du reste (reste de Lagrange, reste de Young, reste sous forme intégrale). Comparaison des fonctions au voisinage d'un point. Développements limités, développements asymptotiques. Notation o et O de Landau ;

2. Fonctions vectorielles d'une variable réelle : dérivation, théorèmes des accroissements finis, formules de Taylor ;

3. Différentielle d'une application d'un espace d'un espace vectoriel normé dans un autre. Théorème des fonctions composées : exemples des applications multilinéaires. Applications de Rn dans Rp : dérivées partielles, matrice jacobienne. Application au problème du changement de variables. Classe C1 des fonctions continûment différentiables sur un ouvert, sa caractérisation en termes de dérivées partielles ;

4. Classe Ck des applications k fois continûment différentiables sur un ouvert. Dérivées partielles d'ordre supérieur : interversion de l'ordre des dérivations. Formules des accroissements finis, formule de Taylor ;

5. Fonctions implicites, existence, continuité, différentiation. Théorème d'inversion locale. Théorème des fonctions implicites. Théorème des extrêma liés en dimension finie ;

6. Fonctions de plusieurs variables réelles à valeur dans R : convexité, extremum local.

III. Calcul intégral

1. Tribus, mesures positives, mesures de Lebesgue : applications mesurables, intégrables ;

2. Convergence dominée. Théorèmes de convergence des intégrales dépendant d'un paramètre ;

3. Mesure produit, théorème de Fubini ;

4. Espaces LP ;

5. Changements de variables dans Rn.

IV. Séries

1. Séries à termes réels ou complexes : convergence, somme. Cas des séries à termes positifs : comparaison de deux séries, comparaison d'une série et d'une intégrale. Convergence absolue. Produit de deux séries absolument convergentes. Séries doubles, produits infinis. Séries vectorielles (dans un espace de Banach). Convergence normale. Calcul approché de la somme d'une série ;

2. Suites et séries de fonctions numériques, convergence simple, convergence uniforme, convergence normale d'une série ; application à l'étude de la continuité de la dérivabilité, de l'intégrabilité d'une fonction définie par une suite ou une série.

3. Séries entières. Rayon de convergence. Somme du produit de deux séries entières. Convergence uniforme, continuité ;

4. Série de Taylor, développement de fonctions en séries entières ;

5. Développement en série entière des fonctions usuelles. Fonctions exponentielles complexes ;

6. Séries de Fourier. Coefficients et série de Fourier d'une fonction. Théorèmes de Fejer et Dirichlet. Convergence normale de la série de Fourier d'une fonction continue de classe C¹ par morceaux. Théorie L² des séries de Fourier.

V. Équations différentielles

1. Equations différentielles de la forme x'=f(t,x), t dans un intervalle de R, x dans un ouvert de R^n. Théorème de Cauchy-Lipschitz. Solutions maximales. Lemme de Gronwall. Critère de sortie de tout compact (théorème « des bouts ») ;

2. Systèmes différentiels linéaires. Méthode de variation des constantes (formule de Duhamel). Cas des coefficients constants. Application à la résolution d'équations linéaires d'ordre supérieur à 1.

VI. Analyse à une variable complexe

1. Fonctions holomorphes. Conditions de Cauchy-Riemann. Intégrale d'une fonction continue le long d'un chemin C 1 par morceaux. Primitives d'une fonction holomorphe. Déterminations du logarithme. Théorème d'holomorphie sous le signe intégrale ;

2. Indice d'un chemin fermé C 1 par morceaux par rapport à un point ;

3. Formules de Cauchy. Analyticité d'une fonction holomorphe. Principe des zéros isolés. Principe du prolongement analytique. Principe du maximum ;

4. Singularités isolées. Fonctions méromorphes. Théorème des résidus ;

5. Suites et séries de fonctions holomorphes. Stabilité de l'holomorphie par convergence uniforme.

VII. Algèbre générale

1. Vocabulaire de la théorie des ensembles. Produits de deux ensembles. Applications d'un ensemble dans un ensemble. Composition des applications. Restriction, application réciproque. Image, image réciproque. Applications injectives, surjectives, bijectives. Permutations d'un ensemble. Relations d'ordre. Relations d'équivalence. Ensemble N des entiers naturels. Cardinal d'un ensemble fini ou dénombrable. Nombre de parties de cardinal fini dans un ensemble de cardinal n ;

2. Groupes. Homorphismes de groupes. Sous-groupes. Classes d'équivalence modulo un groupe. Sousgroupes distingués : groupes quotients. Sous-groupe engendré par une partie. Groupes monogènes. Ordre d'un élément. Opération d'un groupe sur un ensemble : orbites, stabilisateurs. Groupes abéliens. Groupe symétrique : décomposition en cycles : signature d'une permutation ; groupe alterné ;

3. Anneaux. Homorphisme d'anneaux. Sous-anneaux. Anneaux commutatifs ; formule du binôme. Divisibilité dans les anneaux commutatifs intègres : éléments irréductibles : éléments associés. Anneaux factoriels : plus grand diviseur commun, plus petit multiple commun. Anneaux principaux ; théorème de Bezout. Anneaux euclidiens : algorithme du calcul du plus grand diviseur commun dans un anneau euclidien. Anneaux Z des entiers relatifs, division euclidienne, Z/nZ, indicateur d'Euler, bases de numération. Algèbre sur un anneau commutatif. Algèbre des polynômes à une ou plusieurs indéterminées sur un anneau commutatif intègre. Algèbre des fonctions polynomiales. Expression d'un polynôme symétrique à l'aide des polynômes symétriques élémentaires ; formule de Newton. Racines d'un polynôme à une indéterminée, multiplicité, relations entre coefficients et racines ;

4. Théorie des corps. Corps (commutatifs), sous-corps, corps premier, caractéristique. Corps des fractions d'un anneau commutatif intègre. Corps des fractions rationnelles à une indéterminée, sur un corps (commutatif). Décomposition d'une fraction rationnelle en éléments simples. Corps Q des nombres rationnels. Corps R des nombres réels. Corps C des nombres complexes. Théorème de d'Alembert-Gauss ;

VIII. Algèbre linéaire et bilinéaire

1. Espaces vectoriels. Sous-espaces vectoriels. Applications linéaires, image, noyau. Somme de sous-espaces vectoriels, somme directe ;

2. Espaces vectoriels de dimension finie. Bases, dimension. Supplémentaires d'un sous-espace, rang d'une application linéaire. Théorème du rang. Espace dual, espace bidual : transposée d'une application linéaire : orthogonalité. Base duale. Rang de la transposée. Isomorphisme entre un espace et son bidual. Matrices : opérations sur les matrices. Matrice d'un endomorphisme relativement à une base : changement de base. Rang d'une matrice, rang de sa transposée. Déterminant d'une matrice et d'un endomorphisme. Matrice des cofacteurs. Trace d'une matrice et d'un endomorphisme. Résolution d'un système d'équations linéaires : rang du système, compatibilité, formules de Cramer. Réduction d'un endomorphisme : polynôme minimal et caractéristique d'un endomorphisme. Diagonalisation, trigonalisation. Théorème de Cayley-Hamilton ;

3. Algèbre bilinéaire. Généralités sur les formes bilinéaires symétriques sur un espace vectoriel de dimension finie (la caractéristique du corps étant supposée différente de 2) : rang, signature, théorème de Sylvester, orthogonalité, matrice relativement à une base et changement de base, discriminant. Existence d'une base orthogonale. Classification des formes quadratiques sur R et C. Espaces vectoriels euclidien. Produit scalaire, inégalités de Cauchy-Schwarz, norme euclidienne. Adjoint d'un endomorphisme. Groupe orthogonal : description des éléments et dimension 2 et 3. Réduction des endomorphismes orthogonaux et symétriques. Espaces vectoriels hermitiens. Produit hermitien, norme hermitienne. Adjoint d'un endomorphisme. Groupe unitaire. Réduction des endomorphismes normaux.

IX. Géométrie

Géométrie affine. Espaces affine et espace vectoriel associés de dimension finie. Barycentres. Repères affines. Applications affines. Sous-espaces affines. Équations d'un espace affine. Géométrie affine euclidienne plane. Notion d'angle. Coordonnées polaires. Similitudes. Géométrie affine euclidienne en dimension trois. Coordonnées cylindriques et sphériques.

X. Probabilités

1. Notions de base : espaces de probabilité (discrets et non discrets), vecteurs et variables aléatoires, lois jointes et lois marginales, inégalités classiques, usage des moments, des fonctions caractéristiques et des fonctions génératrices, convergences (en moyenne d'ordre p, presque sûre, en probabilité, en loi) ;

2. Indépendance : tribus indépendantes, variables aléatoires indépendantes, loi du zéro-un, Borel-Cantelli, loi faible des grands nombres, théorème limite central.

 

Article 17 - Chimie

ÉPREUVE ÉCRITE D'ADMISSIBILITÉ

Chimie générale

Le programme de l'épreuve porte sur les enseignements de chimie organique, chimie inorganique et de chimie physique couramment dispensés en licence de chimie.

ÉPREUVES ORALES ET PRATIQUES D'ADMISSION

Travaux expérimentaux de chimie

L'épreuve est d'une durée globale de 4 heures et est composée de deux parties distinctes de 2 heures, de poids égal dans la notation. Du matériel classique de laboratoire et certains produits, solutions ou solvants sont mis à disposition du candidat. Les sujets proposés consistent en une problématique ouverte et contextualisée. Le candidat doit proposer une démarche expérimentale afin de pouvoir résoudre la ou les questions posées. Après discussion, le candidat met en œuvre un protocole visant à résoudre le problème posé. Il doit faire preuve de son aptitude à concevoir, conduire puis interpréter les expériences de chimie entreprises.

Interrogation de chimie et entretien

Cette interrogation est d'une durée globale d'une heure.

Une partie consiste en la résolution de problèmes portant sur le programme de l'épreuve écrite. Elle a pour but d'apprécier non seulement les connaissances du candidat, mais aussi ses aptitudes à l'organisation du raisonnement scientifique et à l'exposé de ses idées.

La deuxième partie d'épreuve est un entretien au cours duquel le candidat doit présenter et motiver son projet de formation à court et moyen termes. Afin de préciser ce dernier, le candidat peut s'il le souhaite venir avec une copie de maximum 3 transparents pour les membres du jury. Cet entretien a pour objectif d'évaluer l'adéquation du projet personnel du candidat avec la formation proposée dans le département de chimie de l'ENS Paris-Saclay ainsi que ses motivations quant à la carrière qu'il souhaite poursuivre.

 

Article 18 - Biologie

ÉPREUVES D'ADMISSION

Épreuve d'analyse d'articles scientifiques

Cette épreuve a pour but d'apprécier l'aptitude des candidats à comprendre et à présenter des articles scientifiques publiés dans des revues internationales à comité de lecture et portant sur des problématiques relatives aux sciences du vivant.

Interrogation-entretien

1re partie : Interrogation orale sur un sujet imposé

Cette épreuve a pour but d'apprécier non seulement les connaissances du candidat mais aussi ses aptitudes à l'organisation du raisonnement scientifique et à l'exposé de ses idées. Elle se termine par un entretien.

Le programme de l'épreuve porte sur les enseignements usuels de licence. En particulier, des connaissances approfondies sont attendues dans les domaines suivants : biochimie, génétique moléculaire, physiologie humaine, neurobiologie, biologie cellulaire, immunologie, virologie et microbiologie. Une intégration des différents niveaux d'échelle (des molécules aux cellules puis à l'organisme) peut être demandée. Les candidats doivent posséder des connaissances fondamentales du meilleur niveau et actualisées dans ces domaines, mais doivent également être capables d'expliquer les démarches expérimentales ayant permis de les établir.

2e partie : Interrogation portant sur un texte traitant des aspects éthiques, philosophiques ou sociétaux de thèmes touchant à la science ou à la médecine et aux progrès qui leur sont associés.

3e partie : Entretien

Cet entretien a pour objectif d'évaluer l'adéquation du projet personnel du candidat avec la formation proposée dans le département de biologie de l'ENS Paris-Saclay ainsi que ses motivations quant à la carrière qu'il souhaite poursuivre.

 

Article 19 - Physique

Interrogation de physique

Le programme de l'épreuve réunit les programmes de licence de physique.

 

Article 20 - Informatique

L'épreuve orale disciplinaire du concours d'admission en deuxième année en informatique porte sur les connaissances de base au programme des licences d'informatique.

En particulier, des connaissances approfondies sont attendues dans les domaines suivants :

a) architecture des machines et systèmes d'exploitation ;

b) algorithmique et structures de données ;

c) théorie des langages ;

d) calculabilité et complexité ;

e) programmation et compilation ;

f) sémantique et logique.

 

Article 21 - Sciences de l'ingénieur

L'épreuve pratique porte sur les thématiques de la spécialité choisie à l'inscription.

I. Physique appliquée à l'électricité

Les domaines suivants de la physique appliquée à l'électricité peuvent être abordés au cours de cette épreuve :

• électromagnétisme ;
• électrostatique ;
• électrocinétique ;
• thermodynamique.

Par ailleurs les candidats sont évalués sur leur capacité d'analyse des circuits électriques de base et les moyens de contrôle de processus.

II. Mécanique

Les domaines suivants de l'ingénierie mécanique peuvent être abordés au cours de cette épreuve :

• outils de communication technique et d'analyse fonctionnelle ;
• mécanique des solides rigides et des systèmes ;
• mécanique des milieux déformables solides et fluides ;
• mécanique des structures et éléments finis ;
• matériaux ;
• automatique industrielle ;
• asservissement ;
• industrialisation.

Par ailleurs une attention particulière est donnée à la culture technologique des candidats sur des domaines tels que :

• technologie de construction ;
• transmission de puissance ;
• choix des composants classiques et dimensionnements associés ;
• capteurs et techniques de mesures ;
• procédés de fabrication ;
• systèmes automatisés.

Les candidats sont interrogés sur les programmes de licences de sciences de l'ingénieur (unités d'enseignement à connotation mécanique). Les compétences évaluées sont liées à l'aptitude du candidat maîtriser les modélisations et les techniques expérimentales.

III. Génie civil

Les candidats sont interrogés sur les aspects scientifiques développés dans les programmes de licence, avec une attention particulière sur les thématiques suivantes :

• comportement et résistance des matériaux ;
• mécanique (solide-fluide) ;
• thermodynamique et thermique.

Selon les parcours d'origine des étudiants, les thèmes abordés reprennent :

• le comportement mécanique d'ouvrages de génie civil (béton, acier, sols et roches) ;
• les procédés de construction ;
• les technologies applicables au domaine du génie civil (structures et/ou équipements techniques) ;
• les transferts (thermiques-fluides) appliqués au bâtiment.

 

Article 22 - SHS (sciences humaines et sociales)

ÉPREUVE ORALE DISCIPLINAIRE À OPTION

L'épreuve se prépare sur dossier comportant divers documents propres à l'option choisie parmi les 4 possibilités offertes : sociologie, économie, gestion, histoire.

Les thèmes couverts sont :

• option sociologie : objets, concepts et modes de raisonnement en sociologie ;
• option économie : objets, concepts et modes de raisonnement en économie ;
• option gestion : analyse et débat sur les problèmes managériaux des organisations ; utilisation des outils et méthodes de gestion pour les décisions des organisations ;
• option histoire : grands enjeux historiographiques en histoire contemporaine.

 

Article 23 - Anglais

L'exposé porte sur un dossier thématique comprenant plusieurs documents en lien avec l'anglais de spécialité.

L'épreuve porte sur un des points suivants : les styles spécialisés en contexte anglophone ; la phraséologie spécialisée en contexte anglophone ; l'analyse des besoins, l'ingénierie des cours d'anglais en secteur Lansad (langues pour spécialistes d'autres disciplines), l'évaluation en secteur Lansad ; la fiction à substrat professionnel ; les genres discursifs spécialisés en contexte anglophone.

 

Article 24 - Design

Épreuve écrite de synthèse, projet et soutenance

Ces épreuves d'admission s'inscrivent dans un lieu d'étude commun imaginé par les concepteurs et constituent les 3 phases d'une même démarche allant de la réflexion au développement d'un projet de graphisme, d'espace, de produit ou de service puis de sa soutenance devant un jury.

L'étude et synthèse de texte propose un questionnement faisant appel tant à la philosophie, à l'histoire du design, qu'à la connaissance de l'actualité de la discipline. Cette étape de l'épreuve doit donner lieu à une prise de position argumentée définissant le champ de problématique envisagé que le candidat développera dans la suite de l'épreuve.

Le projet de design où le lieu d'étude est le contexte d'un projet de graphisme, d'espace, de produit ou de service. Un ensemble de paramètres de contexte par discipline est fourni au candidat qui sera libre de choisir sa spécialisation. Le rendu se fera sous forme de planches A3.

La soutenance orale du projet, où le candidat aura accès au portfolio déposé pour la phase d'admissibilité.

Épreuve orale de langue anglaise

Présentation et commentaire d'un texte général ou artistique issu de revues spécialisées dans un domaine du design, suivis d'une conversation.

Titre III. Dispositions finales

Article 25 - L'arrêté du 21 novembre 2018 fixant les programmes des concours d'admission en première année et en cycle master est abrogé.

 

Article 26 - Le présent arrêté entre en vigueur pour la session des concours 2023.

 

Article 27 - L'administrateur provisoire de l'École normale supérieure Paris-Saclay est chargé de l'exécution du présent arrêté, qui sera publié au Bulletin officiel du ministère de l'enseignement supérieur et de la recherche.

 

Fait le 26 octobre 2022